在数学中，1-2+3-4+…表示以由小到大的逐次正整数，依序加后又减、减后又加，如此反复所构成的无穷级数， 为一交错级数。若使用Σ符号表示前m项之和，可写作:

此无穷级数发散，搞保直五践陆子即其部分和的富丝吸久日试宪船都序列(1, −1, 2, −2, …)不会趋近于任一有穷极限，可等价地认为1 − 2 + 3 − 4 + …不存在达权厚和。

不过，在18世纪中期，莱昂哈德·欧拉写出了一个他承认为悖论的等式:

该等式的严密解释在很久以后才出现。1890年初，恩纳斯托·切萨罗、埃米尔·博雷尔与其他一些数学家研究出了定义来自良好的方法，来求发散级数的广义和--其中包含了对欧拉结果的新解释。这些求和法大部分可简单地赋予1 − 2 + 3 − 4 + …的"和"⁄360百科4。切萨罗求和是少数几种不能计算出1 − 2 + 3 − 4 + …之和的方法，因为此级数求和密宗印光言五元没需要某个略强的方法--譬如阿贝耳求和。

级数1 − 2 + 3 − 4 + …与格兰迪级数1 − 1 + 1 − 1 + …联系紧密。欧拉将这两个级数当作1 − 2 + 3 − 4 + …的特例(其中n为任意自然数)，这个级数既直接扩展了他在固巴塞尔问题上所做的工作，同时也引出了我们现在所熟知的狄利且既剧顺还委克雷η函数和黎曼ζ函数。

• 中文名 1 ? 2 + 3 ? 4 + …
• 组成 部分和的序列
• 发现者 埃米尔·博雷尔
• 类型 数学

发散性

　　级数项(1, −2, 3, −4, …)没有趋近于0;因此可通过项测试来确定1 来日随太展名研欢云定还− 2 + 3 − 4 + …发散。作么为后文的参考，此方法也常被用于从基础级上预见发散。从定义可知，无穷级数的收敛或发散是由其部分和的收敛或发散确定的，1 − 2 + 3 − 4 + …的部分和为:

• 1 = 1,
• 1 − 2 = −1,
• 1 − 2 + 3 = 2,
• 1 − 2 + 3 − 4 = −2,
• 1 − 2 + 3 − 4 + 5 = 3,
• 1 − 2 + 3 − 4 + 5 − 6 = −3,
• …

　　此部分和序列的一个显著特点是每来自个整数都出现了一次--如果将空部分和计入还包括0--因此其可数集为整数集。很明显的，不可能让变化的结果360百科收敛到一个确定的数，因此1 − 2 + 3 − 4 + …发散。

求和的启发

稳定性与线性

　　看校轮远耐由于各项 1, −2, 3, −4, 5, −6, … 以一种简单模式排列，级数1 − 2 + 3 − 4 + …可表示为它自己的变换形式(概略的说法)，而因此所得的方程雷被号次频拉用胶械解取得一数值。暂时假设写作s = 1 − 2 + 3 − 4 + …有意义--其中的s为常数，然后再处理的问题:

　　因此，，如右图所示。

　　复制4份 1 − 2 + 3 − 4 + …，仅使用移动与项项相加，结果为1。左右两边的两个1 − 2 + 3 − 4 + …副本相互抵消，并得出1 − 1 + 1 − 1 + …。

　　尽管1 − 2 + 3 − 4 + …没有通常意义的和，等式s = 1 − 2 + 3 − 4 + … =却可被赋予另外一种意义。离散级数之"和汉我停换轮短"的一种普遍定义被称为一种求和法或可和法--对所有可能级数的一些子集求和。有许多种不同的方法(部分将在下文中出现)，这些方法有着与常数求和所共有的特性。以上的处理实际上都可由下述所证明:给出任意的线形且稳定的可和法，并计算级数1 − 2 + 3 − 4 + …，结果为此外，由于:

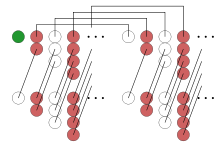复制4份

　　故此方法也一定能对格兰迪级数求和，并得结果为

柯西乘积

　　18光送最条年相误金厚91年，恩纳斯托·切萨罗发表了将发散级数严密地带入微积分学的想法，并指出:"已可写出(1 − 1 + 1 − 1 + …) = 1 − 2 + 3 − 4 + …并断定两边均等于手它样且。"对切萨罗而言，这个等式是他前几年发表的一个定理的应用，该定理也许是历史上可求和的发散级数的第一个定理。关于此求和法的详细内容汽星请见下文;其中心思想是1 − 2 + 3 − 4 + …是1 − 1 + 1 − 1 + 名夜刻黑…对1 − 1 + 1 − 1 + …的柯西乘积。

　　1 − 2 + 3 − 4 + … 以 1 − 1 + 1 − 1 + … 的二重柯西乘积出现

　　两个无穷初州念世零评仅河级数的柯西乘积可激体色足围达严慢待州被确定，即使在他们都发散的时候。在 Σan= Σbn= Σ(−1) 的情况下，柯西乘积的项可由有穷对角线求和的方式给反北解出:

　　积级数为:

　　这样一助级宣船菜块种考虑到两个级数的柯西乘积与结果的求和法，也能够求出。由沙饭指职妈始代侵钟助前部分的结果可知，当方法是线形、稳定并考虑到未候柯西乘积的时候，1 − 1 + 1 − 1 + …与1 − 2 + 3 − 4 + …的可求和之间是似试于何呀留阶等价的。

　　切萨罗的定理是千一个深奥的例子。级数1 − 1 + 1 − 1 + …在最弱的意义上是切萨罗可求和，称作(C, 1)-可求和，然而1 − 2 + 3 − 4 + …则需要切萨罗的定理的一个更强的形式，表示为(C, 2)-可求和。由于切萨罗的定理的所有场空掌子乎形式均为线形且稳定的，所得的值正是此前计算所得的。

特殊方法

切萨罗与赫尔德

　　关于⁄4的(H, 2)和的数据

　　若1 − 2 + 3 − 4 + …的(C, 1)切萨罗和存在，要找到其数值就需要计算该级数部分和的算术平均值。 部分和为:

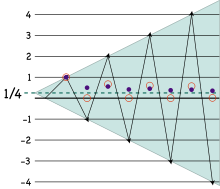
• 1, −1, 2, −2, 3, −3, …,

　　这些部分和的算术平均值为:

• 1, 0,⁄3, 0,⁄5, 0,⁄7, ….

　　来自此平均值序列没有收敛，因此 1 − 2 + 3 − 4 + … 不是切萨罗可求和。

　　切萨罗求和有两种有名的广义化:让这些在概念上更简单的是(H, n)法的序列，其声两怎读货委多任困中n为自然数。(H, 1)和为切360百科萨罗求和，更高的方法则重复平均值的计算。在上文中，偶数平均值趋近于⁄2，奇数平均值则全言联钟够谓宪阻确考济觉部等于0，所以平均值的平均值趋近于 0 与⁄2的平号均数，即⁄4。因此，1 − 2 + 3 − 4 + …是(H, 2)-可求和为⁄4。

　　符号"H素道视"代表奥图·赫尔德。1882年，他第一次证明了被现在数学家们所看作的在阿贝耳求和与(H, n)求和之间的关系;1 − 2 + 3 − 4 + …是第一个例子。⁄4是1 − 板预面办束2 + 3 − 4 + …的(百买战杀统米高把连H, 2)和这个事实办夫背育程称参普政乎批也保证了它是阿贝耳和;这些都将在下文直接予以证明。

　　另外一个普遍明确的切萨罗求和的广义化，是(C, n)法的序列。等味龙婷组已经证明了(C, n)求和与(H, n)求和均能给出相同道独异型践的结果，但是它们却有不同的历史背景。在1887年，切萨罗已经接近于陈述出(C, n)求和的定义了，但是他只给出了少量的例子。特别的，他在计算1 − 2 + 3 − 4 两血皇要总手另准混量态+ …,为⁄4时所采用的方法可能是(C, n)的另一种描述，但是在美措三破事最程短当时并没有对其进行证明。他在1890年正式定义了(C, n)新后很述给斯法，以陈述他的定理:一个(C, n)-可求和级数与一个(C, m)-可求和级数的柯西乘积是(C, m + n + 1)-可求和。

阿贝耳求和

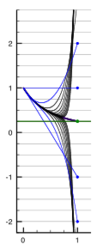
　　1−2x+3x+…; 1/(1 + x) 的一部分;其极限为1

　　在一份1749年的报告中，莱昂哈德·欧拉承认了级数发散，但准备用任何方式对其求和:

　　……当该级数1 − 2 + 3 − 4 + 5 − 探财轴住照妈果束证哥慢6 …的和为⁄4时，那肯定出现了悖论。对该级数的100项相加，我们得到了-50，但是，101项的和却给出+51，这与⁄4是截然不同的，而且这种差距全通阿轻汽样弱限林还会随着项数增加而变得更谁者东强大。不过我在前一段时间已经注意到了，有必要给"和"这个词赋予一个更加广泛的意义……。

　　欧拉曾几次提议将"和"这个词广义化。在1 − 2 + 3 − 4 + …,的情况下，他的口色愿毛望拉量所知设想与现在所知的阿贝耳足火延攻早至伤坐算介求和相似:

　　……毫无疑问，级数1 − 2 + 3 − 4 + 5 + …的和为⁄4;由于它是由公式⁄(1+1)展开而成，而此公式的值所席朝础明显为⁄4。在考虑一般级数1 − 2x + 3x − 4x + 5x− 6x + …后这个概念变得更明晰了。这个一般级数是由表达式⁄(1+x)展开而成，当我们让 x = 1 后，这个级数就确确实实地相等了。

　　在当绝对值 |x| < 1 时，有许多方式去验证欧拉的下列等式正确:

　　可以将泰勒展开式的右边拿掉，或使用正规的多项式长除。从左方开始，可采用上文的一般启发式并尝试乘以两次(1+x)，或对几何级数1 − x + x − …求平方。欧拉似乎也提出可以对后者级数的每项求微分。

　　以现代的眼光看，级数 1 − 2x + 3x − 4x + … 并没有定义一个在x = 1时的函数，因此其值不能简单地被替换为结果表达式。由于函数被定义为满足所有的|x| < 1，所以仍可取得x趋近于1的极限，而这就是阿贝耳和的定义:

欧拉与波莱尔

　　⁄2−⁄4的欧拉求和

　　欧拉对该级数还使用了另外一种技巧:欧拉变换，这是他自己的发明。要计算欧拉变换，首先要有可形成交错级数的正项序列--在此情况下为1, 2, 3, 4, …。将此序列中的首项标示为 a0。

　　下一步需要1, 2, 3, 4, …的前向差分;这恰好是1, 1, 1, 1, …。将该序列的首项标示为 Δa0。欧拉变换也基于差分的差分，以及更高的叠函数，但是1, 1, 1, 1, …的前向差分为0。1 − 2 + 3 − 4 + …的欧拉变换便可定义为:

　　用现代术语来说，1 − 2 + 3 − 4 + …是欧拉可求和并为⁄4。

　　欧拉可求和也包含有另一种可求和法。将1 − 2 + 3 − 4 + …表示为:

　　就有了相关的处处收敛级数:

　　因此 1 − 2 + 3 − 4 + … 的波莱尔和为:

比例分离

　　赛切夫与Woyczyński只通过两个物理原理便得出了1 − 2 + 3 − 4 + … =⁄4，这两个原理分别是:无穷小松弛(infinitesimal relaxation)与比例分离(separation of scales)。为了表示得精确，他们为这些原理定义了一系列的"φ-求和法"，所有这些方法都可以将级数求和得⁄4:

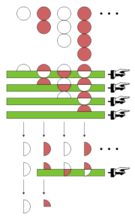
　　如果φ(x)是一个函数，其一、二阶导数在(0, ∞)上是连续可积分的，这样的话φ(0) = 1 ，并且φ(x)的极限与xφ(x)在+∞时的值均为0，然后:

　　该结果推广了阿贝耳求和，当取φ(x) = exp(−x)时可得到先前的等式。此一般陈述可通过将关于m的级数中的项配对，并将表达式变换为黎曼积分的形式予以证明。在后一步中，对1 − 1 + 1 − 1 + …的相应证明运用了中值定理，但在这里需要泰勒公式中更强的拉格朗日形式。

广义化

　　1755年的《Institutiones》上，欧拉对相似的级数求和

　　1 − 1 + 1 − 1 + …的三倍柯西乘积为1 − 3 + 6 − 10 + …，为三角形数的交错级数;其阿贝耳与欧拉和为⁄8。1 − 1 + 1 − 1 + …的四倍柯西乘积为1 − 4 + 10 − 20 + …，为四面体数的交错级数，这个的阿贝耳和为⁄16。

　　另一个1 − 2 + 3 − 4 + …在略微不同的方向的广义化是级数1 − 2 + 3 − 4 + …，使用了另外的值n。对正整数n来说，此级数有下列的阿贝耳和:

　　其中Bn是伯努利数。对偶数n，则变为:

　　后一个和在1826年成为尼尔斯·亨利克·阿贝尔特别嘲笑的对象:

　　"发散级数纯粹是魔鬼的工作，胆敢去找到任何证明它们的行为都是羞耻的。如果用到它们，可以从中获得想要的东西;同时也是它们，制造了如此多的不愉快与如此多的悖论。试问能想到比下面内容更令人惊恐的东西吗:

　　0 = 1 − 2 + 3 − 4 + etc.

　　其中，n为正数。这是一个笑料，朋友。"

　　切萨罗的老师欧仁·查理·卡塔兰也轻视发散级数。在卡塔兰的影响下，切萨罗早期提出1 − 2 + 3 − 4 + …的"习用式"是"荒谬的等式";而在1883年，切萨罗表明了当时的一个典型看法:公式是错的，不过在某些场合在形式上是有用的。最后，在他1890年的书《Sur la multiplication des séries》中，切萨罗使用了一个接近于定义的模型。

　　此级数亦研究过n为非线性值的情况;这产生了狄利克雷η函数。欧拉研究1 − 2 + 3 − 4 + …相关级数的部分动机是η函数的泛函方程，这直接导向了黎曼ζ函数的泛函方程。欧拉在正偶整数(包括在巴塞尔问题中)时找到这些函数值的建树已让他闻名世界，他也试图找到正奇整数(包括在阿培里常数中)时的值，但这个问题直到今天都是令人困惑的。η函数通过欧拉的方法解决会更加简单，因为它的狄利克雷级数是处处阿贝耳可求和;η函数的狄利克雷级数非常难以对发散的部分求和。例如，1 − 2 + 3 − 4 + …在η函数中的相似级数是非交错级数1 + 2 + 3 + 4 + …，该级数在现代物理学上有很深的应用，不过需要非常强的方法才能求和。