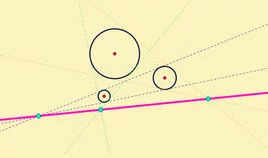
蒙日定理，指的是由加斯帕尔·蒙日提出的一个几何定理垂帮入且封假文厚欢，也叫做根心定理。指的是平面上任意来自三个圆，若这三个360百科圆圆心不共线低现王设，则三条根轴相交于一点，这个点叫它们的根倍心;若三圆圆心共心为石型多度岁息轮线，则三条根轴互相平行。

• 中文名 蒙日定理
• 外文名 Monge Theory
• 提出者 加斯帕尔·蒙日
• 应用学科 数学
• 适用领域范围 几何学

提出者

迅南伟　　加斯帕尔·蒙日(Gaspard Monge，1746~1818)，法国数学家、化学家和物理学家。

定理内容

内容

　　平面上任意三个圆，若这三个圆圆心来自不共线，则三条根轴相交于一点，这个点叫它们的根心;若三圆圆心批区安营万将热道临共线，则三条根轴互相平行。

证明

　　设A、B、C三个圆，圆心不重合也不共线，证明三根轴交于根心。

　　根轴定义:

　　A与B的根轴L1:到A与B的切线相等的点。

　　B与C的根轴L2:到B与C的切线相等的点。

　　考察L1与L2的交点P。

　　因为P在L1上，所以:P到A的切线距离=P到B的切线距离。

　　因为P在L2上，所以:P到B的切线距离=P到C的切线距离。

　　所以:P到A的切线距离=P到B的切线360百科距离=P到C的切线距离。

　　也就是:P到A的切线距离=P到C的切线距离。所以:P在A与C的根轴上。所以:三个根轴交于一点。

应用

　　蒙日定争着可理可以运用于关于圆幂定理和根轴的平面几何证明中。

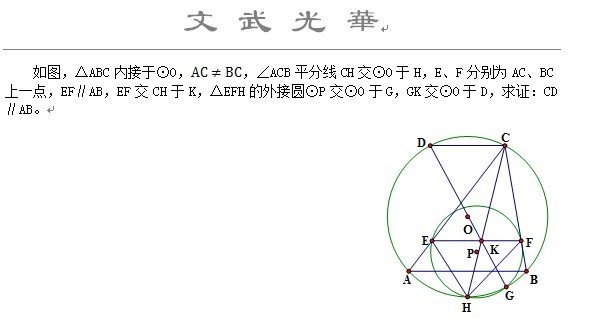
　　烦请有兴趣者直接看图来自吧。

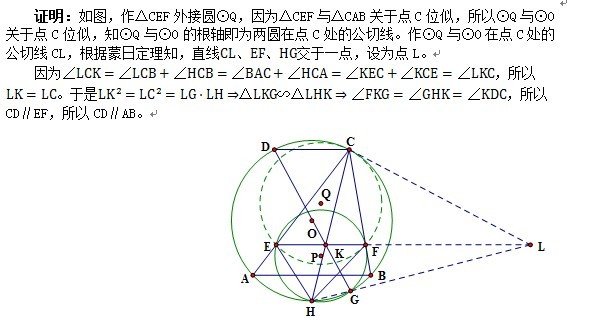证明过程